
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |
|
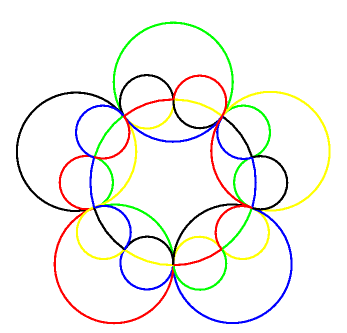
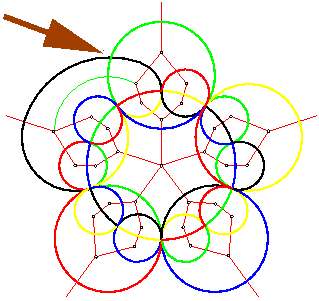
Consider the symmetric 5-venn diagram shown to the left. This diagram can be constructed using
the necklace construction ideas on the page Symmetric Diagrams, Necklaces, and Chains;
it is very non-simple, but it is also not rigid. On this page we show how to transform it into the
unique simple diagram on 5 vertices, shown
at the beginning of the page on symmetric diagrams.
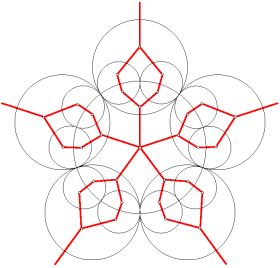
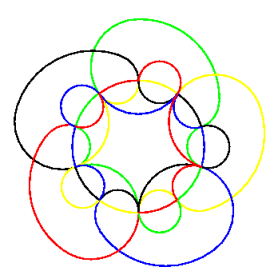
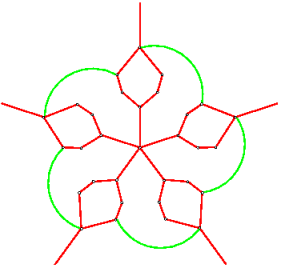
Below we show the corresponding unlabelled Venn dual (the red edges) overlaying a monochromatic version of the diagram to the left, and then the dual graph alone on the right. In both graphs the external vertices, corresponding to the external empty region in the Venn diagram, are identified; we separate them to emphasize the symmetry of the diagram. |
|
|
|
The fact that this can be done without creating any new regions corresponds to the fact that the vertices in the Venn dual corresponding to the newly neighbouring faces can have an edge added between them (i.e. their labels differ by a single bit).
|
|
|
|
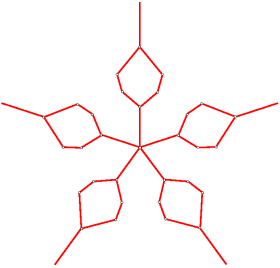
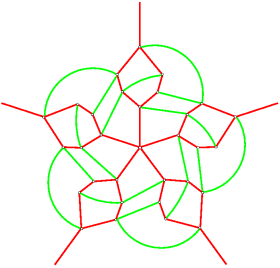
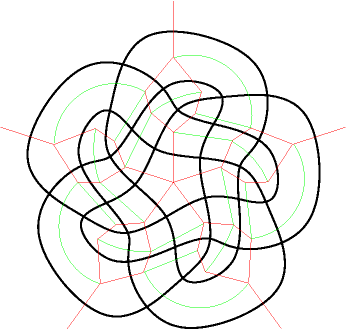
Continuing in this fashion, we add edges to the dual graph until no more can be added; at this point the Venn dual is composed entirely of 4-faces (faces with exactly 4 edges bordering them), implying that the corresponding Venn diagram is simple. Following [KRSW], we can call this operation quadrangulation since each resulting face is a quadrangle. The final diagram is shown below; it is isomorphic to the unique simple symmetric 5-Venn diagram.
|
|

|

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |