
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |
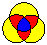
On this page we show many examples of symmetric Venn diagrams for specific values of n. For n = 2, there is only one Venn diagram and it can be drawn to be polar symmetric. For n = 3, there are two symmetric diagrams. The classic three circle diagram is monotone, simple, and has polar symmetry. Diagram #3.1 of Class 1 in the list of all Venn diagrams for n=3 is also a polar symmetric diagram, but it is not simple, nor is it rigid.
The simple ellipse diagram, from [Gr75], has a 5-fold rotational symmetry. It is the only simple symmetric Venn diagram for n=5; here are several different renderings of it:
Here is a non-simple diagram, redrawn from [Gr75], that shows that rectangles can be used - though the figures look like squares, they are slightly longer in one dimension, and in fact Grünbaum conjectured that a 5-Venn diagram of squares does not exist, simple or not.
We have done an exhaustive computer search of all symmetric Venn diagrams for n = 5 (first reported in the 1997 version of this survey). The number of symmetric Venn diagrams for n=5 is 243, and the table below shows the number possessing particular attributes. It is a trivial matter to construct non-simple diagrams from simple ones by "pinching together" simple intersections, but this operation does not produce an essentially different diagram. Thus we are particularly interested in rigid diagrams, of which there are 12+13+2+4 = 31.
| Polar | Rigid | Monotone | Count |
|---|---|---|---|
| no | no | no | 100 |
| no | no | yes | 89 |
| no | yes | no | 12 |
| no | yes | yes | 13 |
| yes | no | no | 5 |
| yes | no | yes | 18 |
| yes | yes | no | 2 |
| yes | yes | yes | 4 |
For n=5, a symmetric minimum Venn diagram must have at least 10 vertices. There are exactly six symmetric rigid Venn diagrams with 10 vertices for n = 5. One of them is shown below. (MinSymm5a.gif, MinSymm5b.gif, MinSymm5c.gif)
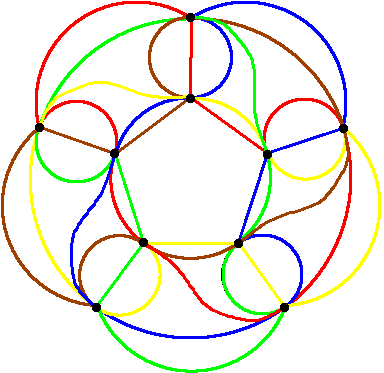
The following table shows the number of symmetric diagrams classified according to the number of vertices and rigidity.
| vertices | 10 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|
| total | 72 | 111 | 49 | 10 | 1 |
| rigid | 6 | 12 | 12 | 0 | 1 |
 Referring to the case n=7, Grünbaum [Gr75,p.19] wrote:
"at present it seems likely that no such diagram exists."
However, Grünbaum himself later found examples of such diagrams
[Gr92b] and
in 1992 additional examples were also discovered by Anthony
Edwards and independently by Carla Savage and Peter Winkler.
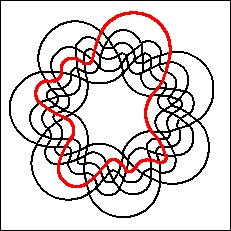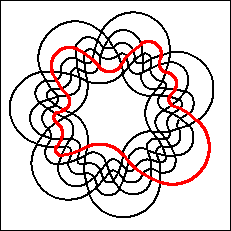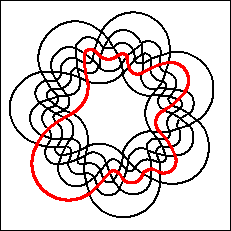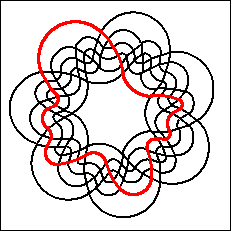
One of Grünbaum's examples is a remarkable
non-monotone simple symmetric Venn diagram.
There are 23 simple monotone symmetric Venn
diagrams for n=7.
Below we summarize what is know about symmetric Venn diagrams for
n=7.
Referring to the case n=7, Grünbaum [Gr75,p.19] wrote:
"at present it seems likely that no such diagram exists."
However, Grünbaum himself later found examples of such diagrams
[Gr92b] and
in 1992 additional examples were also discovered by Anthony
Edwards and independently by Carla Savage and Peter Winkler.
One of Grünbaum's examples is a remarkable
non-monotone simple symmetric Venn diagram.
There are 23 simple monotone symmetric Venn
diagrams for n=7.
Below we summarize what is know about symmetric Venn diagrams for
n=7.
w = z = 142413141324 andOf course, we really only need two of the strings, one starting at the inside and one at the outside, since w can be inferred from x, and y from z -- but it's convenient to have all four, particularly when checking a diagram by hand. How can x be obtained from w in general? Think of the strings as being indexed i = 1,2,...,M. The rule is x[i] = n-w[M-i+1].
x = y = 132414241314.
In fact, only one string is required, since string y is a circular rotation of x. The starting position of y can be determined as the unique position in x where all curves have been encountered an odd number of times (thus implying that we're on the inside of all curves). In the 5 ellipse example, the starting position of y is the rightmost 1 in x. If a single string is chosen to be the representative, then we take the lexicographically least of all four.
This encoding scheme has its parallels in other disciplines: topologists may recognise the Grünbaum encoding as being closely related to the Gauss code of a knot10.
Tao Cao proved in [Cao] that for simple symmetric monotone Venn diagrams the Grünbaum encoding uniquely identifies the diagram (up to isomorphisms).
For n=7, all simple monotone symmetric Venn diagrams with polar symmetry are known; there are six of them, and they are listed below. The first five were discovered by Anthony Edwards using a program to generate candidate diagrams and manual checking to eliminate those candidates that were not Venn diagrams [Ed96]; however one, Hamilton, was found by hand. He named them after the cities in which they were discovered and we follow his naming convention (but also number them P1-P6). Grünbaum [Gr92b] also discovered "Adelaide". An exhaustive computer search by Frank Ruskey uncovered another, "Victoria", that had been overlooked in Edwards' manual checking.
All of the diagram construction methods for non-simple diagrams employed by the author rely on constructing a 1/n pie-slice of the diagram, which is then rotated n times to get the full diagram. Any pie-slice whose boundary doesn't include any intersection points induces a permutation of the curves of the diagram. Since the n-fold composition of that permutation must be the identity and n is prime, it follows that the permutation must be circular. This necessary condition is useful in testing whether a pie-slice could be part of a diagram. Furthermore, if the pie slice is taken so as to not bisect any region, other than the inner and outer regions, then the regions in the pie slice must be inequivalent under rotation. The following page illustrates these ideas more concretely, and shows how they were used by the authors of [GKS] to create a general construction for symmetric Venn diagrams for any n:
| Symmetric Diagrams, Necklaces, and Chains |
From computer searches it is apparent that there are many more non-simple diagrams than there are simple diagrams. Using the above techniques, in [Wes] the authors generated hundreds of thousands of distinct non-simple monotone symmetric 7-Venn diagrams, including 1576 rigid diagrams (both polar symmetric and not).
For n = 7, the value ceiling[ (2n-2)/(n-1) ] is divisible by 7, which leaves open the possibility that there is a minimum vertex symmetric Venn diagram in which every curve passes through every vertex. In fact, we have discovered 60 such diagrams, but all discovered so far are non-rigid. Illustrations of two of them are linked below.
Hamburger and Pippert, in [HP03], using different methods than those above, also constructed a minimum-vertex non-monotone symmetric 7-Venn diagram with several nice features. Their diagram is not rigid either.

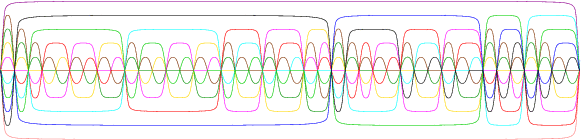
Peter Hamburger [Ha02] constructed the first symmetric Venn diagram for n=11. The diagram is monotone and highly non-simple. It is very similar in form to the diagram for n=7 shown on the symmetric diagrams and necklaces page, but is vastly more complicated because of increase in the the number of regions, intersection points, etc. In fact, the diagram is so intricate that it is difficult to show in a single figure. One sector of the diagram is shown above; the others may be seen on this page. Successive sectors may be obtained from this one by cyclicly permuting the colors.
Linked below are various other renderings of the first symmetric 11-Venn diagram.
The construction method for this diagram uses a partition of the set of all bitstrings of length 11. Recall that the Venn dual can be labelled with bitstrings corresponding to regions, as we discussed on the page Graphs Associated with Venn Diagrams. The construction then uses chains of bitstrings connected together to build the large dual graph of the sector, which then is repeated to give the entire diagram.
Since the diagram is highly non-simple and not rigid, the diagram can be turned in to many others by separating any or all separable vertices. Hamburger has published variants of the diagram with vertex sets from 462 up to 1001 by increments of 11 in [Ha02b]. He and other co-authors have used similar techniques to create other diagrams; see the sub-sections below.
To date, the only other group to have constructed a symmetric 11-Venn diagram is Griggs, Killian, and Savage [GKS]; their diagram is below. The sector forming 1/11th of the diagram is illustrated below; notice that unlike Hamburger's diagrams the sector has a vertical symmetry in that it maps onto itself, ignoring colours, by reflection about a horizontal axis - this is a nice feature of the construction in general.
For n = 11, the minimum possible number of vertices is ceiling[ (211 - 2) / 10 ] = 205. This is not divisible by 11, and the smallest number of vertices possible in a symmetric 11-Venn diagram is 209. In [HS03] Hamburger and Sali extended their above method to produce a diagram with 231 vertices, quite close to the minimum possible, and then later found a diagram with 220 vertices (as yet unpublished - thanks to Peter Hamburger for showing us the diagram). The resulting diagrams are highly non-monotone.
Many of the symmetric 11-Venn diagrams mentioned here, in papers by Peter Hamburger and his co-authors, have been turned into works of art by the artist Edit Hepp. Readers are encouraged to seek out the papers in print to view the diagrams. The processes used to create the artwork are explained in [HH].

|

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |