
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |
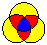
There is a simple symmetric 5-Venn diagram in which each curve is a triangle; see this figure, redrawn from Grünbaum [Gr92b]. Grünbaum [Gr84b] asked whether there was a 6-Venn diagram made from triangles. This question was recently answered in the affirmative by Jeremy Carroll [Car00] - his first example is shown below. The diagrams on this page are all simple. He has subsequently discovered that there are exactly 126 different 6-Venn diagrams that can be drawn where each curve is a triangle.

Below is a table of coordinates for the six triangles.
| (x1, y1) | (x2, y2) | (x3, y3) |
|---|---|---|
| (-69277, -32868) | (135580, 121186) | (70900, 199427) |
| (333561, 225349) | (61764, 76805) | (38980, 182461) |
| (81988, -44426) | (38444, 206222) | (121044, 165111) |
| (-60184, 274046) | (142476, 39903) | (103276, 183962) |
| (131886, 385785) | (38136, 111491) | (94208, 24690) |
| (203271, 9619) | (39604, 82683) | (84652, 206669) |
Below is another nicer example (this jpeg image courtesy of Jeremy Carroll). See his web page [JC] for further examples like this.


|

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |