
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |
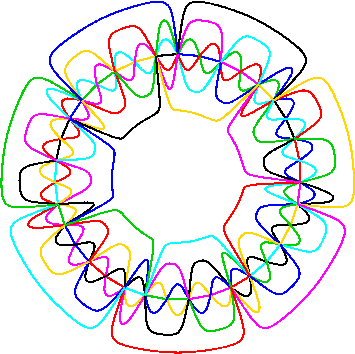
Some monotone symmetric Venn diagrams cannot be constructed sector-by-sector using necklaces. To the
left is a 7-Venn diagram that does not have n vertices through which all curves pass,
and thus it cannot be broken down into 7 sectors. It has the minimum number of vertices for monotone diagrams.
The diagram is rigid, so it is not
isomorphic to any diagram constructable out of sectors. This
diagram is from [Wes].

|

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |