
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |
Since symmetric n-Venn diagrams only exist for prime n, several authors have lamented the fact that while virtually everything is known for n=7, it is very difficult to find out anything about the next case, for n=11. Thus, an interesting line of research is to "bridge the gap" by looking at different notions of symmetry for non-prime numbers of curves.
Consider the 4-Venn diagram below. It is not symmetric, but it has a two-fold symmetry in that the top half, if rotated 180o and relabelled, maps onto the bottom half. Another way of viewing it is that the diagram is composed of 2 copies of the ''pie-slice'' forming the top 1/2 of the diagram, with the curves labelled in the second copy by a permutation by a permutation of the colours in the first pie-slice.
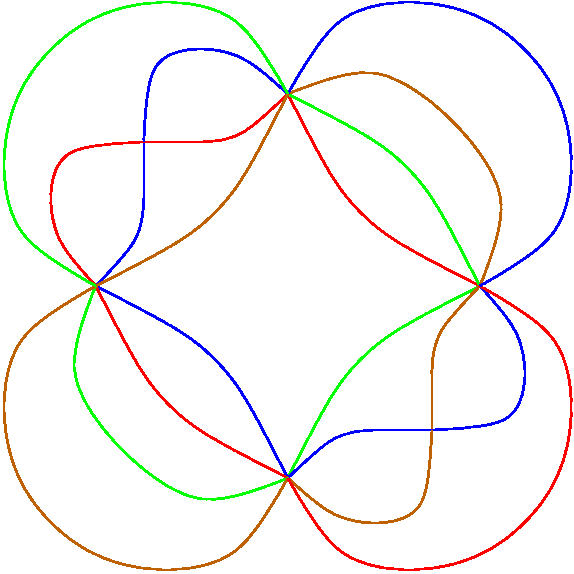
In general, an n-Venn diagram has p-fold pseudo-symmetry if there is a pie-slice making up 1/pth of it so that the rest of the diagram can be generated by repeatedly rotating the pie-slice and recolouring the curves according to a fixed permutation. We then say the diagram is (n,p)-pseudo-symmetric.
The diagram shown is (4,2)-pseudo-symmetric,
and the curves are labelled so that the permutation to be applied is
(1234).
This idea forms a natural extension of traditionally
symmetric Venn diagrams, which can be thought of as being composed of a single pie-slice
forming 1/nth of the diagram rotated n times.
Thus, we can generalise this idea to a Venn
diagram with two parameters, namely n and p, and a
similar process of generating the rest
of the diagram from the pie-slice forming 1/pth of the diagram;
namely copying the pie-slice and rotating the curve labels.
Via a combinatorial argument similar to the proof that n must be prime for
symmetric diagrams to exist, it is easy to show that for (n,p)-pseudo symmetric
diagrams to exist, p must be prime and n must be some power of p
larger than 1.
In [RW], the authors introduced pseudo-symmetry and proved
some interesting properties of pseudo-symmetric diagrams. The most distinctive is
that all of the curves must be distinct in a pseudo-symmetric diagram, whereas
in a symmetric diagram recall that all curves must be congruent.
For example, in the figure above the four distinct curves are:

Ruskey and Weston, in [RW], also constructed, by hand, examples of pseudo-symmetric diagrams for the small cases n = 22 = 4, n = 23 = 8, and n = 32 = 9. The next open case is n = 24 = 16, which is far too large to construct by hand! Details of the method of construction can be found in [Wes]; the authors used a modification of the construction for symmetric n-Venn diagrams in [GKS].
A second nice way to generalise the notion of symmetry to diagrams of n curves with n not being prime is to relax the condition that the diagram must be a Venn diagram, either by adding or subtracting regions to allow symmetry. This notion was introduced by Grünbaum in [Gr99]; since the resulting diagrams are not strictly Venn diagrams we discuss it more on the page Variations and Extensions.
There are many relations between Venn diagrams and (combinatorial) Gray codes. Some of these relations have not much to do with symmetry but some do.
Edwards [Ed92] produced templates for making a rotatable Venn diagram; templates which we have scanned: page 1, page 2, page 3, page 4.
For odd n = 2k+1 the middle two levels problem is to find a Hamilton path in the subgraph of the n-cube induced by those vertices corresponding to k-sets and (k+1)-sets. This is a well-known problem about which several papers have been written ([Jo]). Some symmetric Venn diagrams have embedded in them a solution to the middle two levels problem. For n=7 consider the diagrams Adelaide and Hamilton with the symmetric coloring. The middle two levels correspond to the middle two necklaces, the ones colored yellow (they also have diagonal line shading for those with black-and-white browsers). Note the zig-zag pattern that they follow, alternating between k-sets and (k+1)-sets. This is exactly a solution to the middle two levels problem.

Starting at the set {1}, and writing the bitstring representation of each subset we are lead to the table shown below (read down). Note that: (a) each of the 5 blocks is a right shift of the preceding block, (b) the columns are cyclicly equivalent (under a right shift of 6 bits), and (c) each block contains a representative of each non-trivial necklace of black and white beads. Such Gray codes are obviously balanced in the sense of Bhat and Savage [BS]; that is, each column has the same number of bit changes. It is easy to find symmetric Gray codes for n=7 using any of the Venn diagrams discussed earlier on this page. Gray codes with property (b) are said to be single-track. For more on single-track Gray codes see Hiltgen and Paterson, and Brandestini [HPB].
| 10000 | 01000 | 00100 | 00010 | 00001 |
| 10100 | 01010 | 00101 | 10010 | 01001 |
| 11100 | 01110 | 00111 | 10011 | 11001 |
| 11110 | 01111 | 10111 | 11011 | 11101 |
| 11010 | 01101 | 10110 | 01011 | 10101 |
| 11000 | 01100 | 00110 | 00011 | 10001 |
| Block 1 | Block 2 | Block 3 | Block 4 | Block 5 |
|---|

|

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |