THE ELECTRONIC JOURNAL OF COMBINATORICS 4 (1997), DS #5.

Venn Diagram Survey
Venn Graphs of Venn's General Construction

Here's the Venn graphs of Venn's general construction for n=3,4,5. The red edges indicate the Hamilton cycle that is used in extending to the next higher value of n.

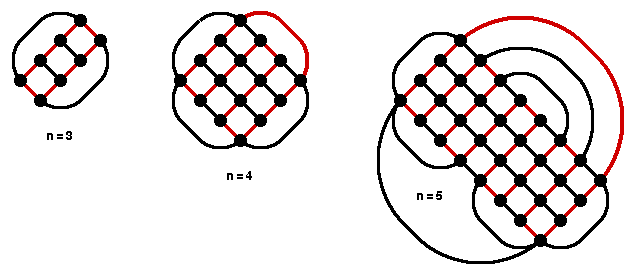
How, in general, do you go from the dual (Venn) graph G of a Venn diagram, together with a Hamilton cycle H in G, and get a new planar dual (Venn) graph G' of a Venn diagram of the next higher order? We now explain this process. Note that H is a simple closed curve with an interior and an exterior.

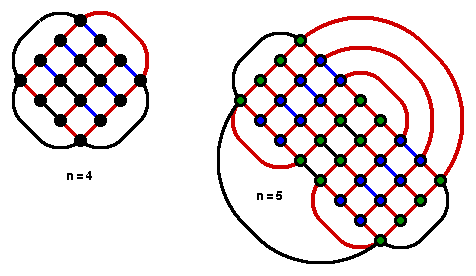
We illustrate the discussion on the expansion of n=4 to n = 5 as shown above. Color the edges of H red, edges on the interior blue, and edges on the exterior black.

• Each (black) vertex of G is split into two vertices, one green and one blue, in G'. The blue vertices are in the interior, the red edges in the exterior.
• Each blue edge in G becomes a blue edge in G' connecting the corresponding blue vertices.
• Each black edge in G becomes a black edge in G' connecting the corresponding green vertices.
• Each red edge in G becomes a 4-cyle of red edges in G', connecting either corresponding vertices or vertices of the same color.

Note that the red edges in G' give the prism of the Hamilton cycle in G.

THE ELECTRONIC JOURNAL OF COMBINATORICS 4 (1997), DS #5.