|
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. March 2001), DS #5. |
Here we (re-)show a Venn diagram made from 5
congruent ellipses.
The regions are colored according to the number
of ellipses in which they are contained: grey = 0, yellow = 1,
red = 2, blue = 3, green = 4, and black = 5.
Note that the number of regions colored with a given color corresponds to
the appropriate binomial coefficient: #(grey) = #(black) = 1,
#(yellow) = #(green) = 5, and #(red) = #(blue) = 10.
This diagram has a very a pleasing symmetry, namely an n-fold rotational symmetry. Such diagrams are said to be symmetric. This simply means that there is a point x about which the diagrams may be rotated by 2 i pi / n and remain invariant, for i=0,1,...,n-1. Any symmetric Venn diagram must be made from congruent curves.
The purpose of this section is to survey what is known about symmetric diagrams. We begin with a simple necessary condition.
Theorem. A necessary condition for the existence of a symmetric n-Venn diagram is that n be a prime number.
To understand why the theorem is true, imagine the diagram to be split evenly into n sectors (pieces of pie). The C(n,k) 1 different regions representing the k-subsets must be evenly distributed in each of the n sectors. It thus follows that n divides C(n,k) for each k = 1,2,...,n-1. This divisibility restriction implies that n must be prime, via a theorem of Leibnitz [Ed96].
Although symmetric diagrams are known for n = 2,3,5,7, and 11 none is known for n = 13 or any larger prime. There is one other symmetry that we will consider for diagrams drawn in the plane.
A symmetric Venn diagram has polar symmetry if it is invariant under "polar flips". Think of the diagram as being projected stereographically onto a sphere with the axis running thru the point of symmetry, and then project the diagram back onto the plane from the antipodal point on the axis. If the corresponding Venn graphs are isomorphic as plane graphs, then the diagram has polar symmetry. The symmetric Venn diagram shown above has polar symmetry, although it is perhaps not readily apparent.
We will now consider specific values of n. For n = 2, there is only one Venn diagram and it can be drawn to be polar symmetric. For n = 3, there are two symmetric diagrams. The classic three circle diagram is monotone, simple, and has polar symmetry. Diagram #3.1 of Class 1 in the list of all Venn diagrams for n=3 is also a polar symmetric diagram, but it is not simple, nor is it rigid.
The ellipse diagram above has a 5-fold rotational symmetry. It is the only simple symmetric Venn diagram for n=5. There are non-simple symmetric diagrams for n=5. The one shown here is a play on the result that Venn diagrams can not be constructed from "curves that are" circles for n > 3; a statement that is no longer true if the three words in quotation marks are removed.
Rick Mabry observes that the link of five knots formed by weaving the Venn diagram shown above is a Brunnian link --- the removal of any knot causes the link to fall apart. Mabry has created a beautiful rendering of the link made from ("ice cream cone curves"). Another one created by the author is here. This diagram serves as an illustration of a symmetric Brunnian link7 of order 5. (The usual depiction of the Borromean rings is a symmetric Brunnian link of order 3.) This Brunnian link is attributed to C. van de Walle by Stewart [St, pg. 106].
We have done an exhaustive computer search of all symmetric Venn diagrams for n = 5. The number of symmetric Venn diagrams for n=5 is 243, and the table below shows the number possessing particular attributes. It is a trivial matter to construct non-simple diagrams from simple ones by "pinching together" simple intersections, but this operation does not produce an essentially different diagram. Thus we are particularly interested in rigid diagrams, of which there are 12+13+2+4 = 31.
| Polar | Rigid | Monotone | Count |
|---|---|---|---|
| no | no | no | 100 |
| no | no | yes | 89 |
| no | yes | no | 12 |
| no | yes | yes | 13 |
| yes | no | no | 5 |
| yes | no | yes | 18 |
| yes | yes | no | 2 |
| yes | yes | yes | 4 |
For n=5, a symmetric minimum Venn diagram must have at least 10 vertices. There are exactly six symmetric rigid Venn diagrams with 10 vertices for n = 5. One of them is shown below. (MinSymm5a.gif, MinSymm5b.gif, MinSymm5c.gif)
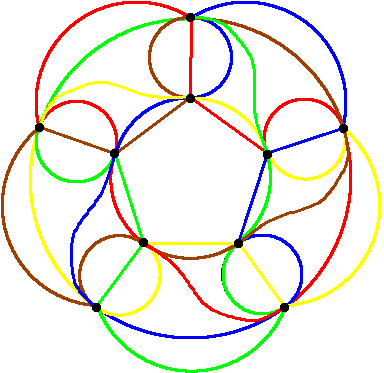
The following table shows the number of symmetric diagrams classified according to the number of vertices and rigidity.
| vertices | 10 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|
| total | 72 | 111 | 49 | 10 | 1 |
| rigid | 6 | 12 | 12 | 0 | 1 |
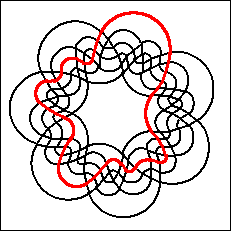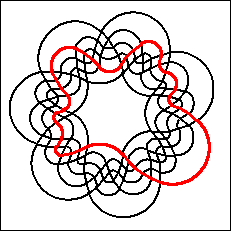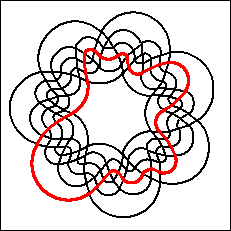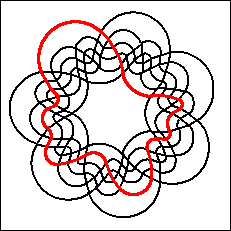Referring to the case n=7, Grünbaum [Gr75,p.19] wrote:
"at present it seems likely that no such diagram exists."
However, Grünbaum found examples of such diagrams
[Gr92b] and
in 1992 additional examples were also discovered by Anthony
Edwards and independently by Carla Savage and Peter Winkler.
One of Grünbaum's examples is a remarkable
non-monotone symmetric Venn diagram.
There are 17 simple monotone symmetric Venn
diagrams for n=7.
Below we summarize what is know about symmetric Venn diagrams for
n=7.
w = z = 142413141324 andOf course, we really only need two of the strings, one starting at the inside and one at the outside, since w can be inferred from x, and y from z -- but it's convenient to have all four, particularly when checking a diagram by hand. How can x obtained from w in general? Think of the strings as being indexed i = 1,2,...,M. The rule is x[i] = n-w[M-i+1].
x = y = 132414241314.
In fact, only one string is required, since string y is a circular rotation of x. The starting position of y can be determined as the unique position in x where all curves have been encountered an odd number of times (thus implying that we're on the inside of all curves). In the 5 ellipse example, the starting position of y is the rightmost 1 in x. If a single string is chosen to be the representative, then we take the lexicographically least of all four.
A closely related encoding is the G-encoding which is obtained by following a curve from the interior/exterior face, numbering and recording the curves in the order that they are encountered. Each string of the encoding is a restricted growth string [COS], meaning that each number is at most one greater than the values that precede it, with the first value being 0 (except that we take the first value to be 1). The four strings corresponding to the 5 ellipse example are:
w = z = 123214121432 and
x = y = 123414341214.
For monotone diagrams the Grünbaum encoding uniquely identifies the diagram, and we believe that this is the case for the G-encoding and non-monotone diagrams.
For n=7, all simple monotone symmetric Venn diagrams with polar symmetry are known; there are six of them, and they are listed below. The first five were discovered by Anthony Edwards using a program to generate candidate diagrams and manual checking to eliminate those candidates that were not Venn diagrams [Ed96]. He named them after the cities in which they were discovered and we follow his naming convention (but also number them P1-P6). Grünbaum [Gr92b] also discovered "Adelaide". An exhaustive computer search by Frank Ruskey uncovered another, "Victoria", that had been overlooked in Edwards manual checking.
From computer searches it is apparent that there are many more non-simple diagrams than there are simple diagrams. We show just a few of them in this section and point out an interesting connection between diagrams and necklaces.
All the diagram construction methods employed by the author, for both simple and non-simple diagrams rely on constructing a 1/n pie-slice of the diagram, which is then rotated n times to get the full diagram. Any pie slice whose boundary doesn't include any intersection points induces a permutation of the curves of the diagram. Since the n-fold composition of that permutation must be the identity and n is prime, it follows that the permutation must be circular. This necessary condition is useful in testing whether a pie-slice could be part of a diagram. Furthermore, if the pie slice is taken so as to not bisect any region, other than the inner and outer regions, then the regions in the pie slice must be inequivalent under rotation. Some of these ideas are illustrated on the following page:
For n = 7, the value ceiling((2n-2)/(n-1)) is divisible by 7, which leaves open the possibility that there is a minimum vertex symmetric Venn diagram in which every curve passes through every vertex. In fact, we have discovered 60 such diagrams, but all discovered so far are non-rigid. Illustrations of two of them may be obtained from the list below.
Recently, Peter Hamburger [Ha01] has constructed a symmetric Venn diagram for n=11. The diagram is monotone and highly non-simple. It is very similar in form to the diagram for n=7 shown on the VennNecklaceEJC.html page above, but is vastly more complicated because of increase in the the number of regions, intersection points, etc. In fact, the diagram is so intricate, that it is difficult to show in a single figure. One sector of the diagram is shown above; the others may be seen on the page VennSymm11EJC.html. Successive sectors may be obtained from this one by cyclicly permuting the colors. Below we show illustrate various other renderings of this diagram.
There are many relations between Venn diagrams and (combinatorial) Gray codes. Some of these relations have not much to do with symmetry but some do.
Edwards [Ed92] produced templates for making a rotatable Venn diagram; templates which we have scanned: page 1, page 2, page 3, page 4.
For odd n = 2k+1 the middle two levels problem is to find a Hamilton path in the subgraph of the n-cube induced by those vertices corresponding to k-sets and (k+1)-sets. This is a well-known problem about which several papers have been written. Some symmetric Venn diagrams have embedded in them a solution to the middle two levels problem. For n=7 consider the diagrams Adelaide and Hamilton with the symmetric coloring. The middle two levels correspond to the middle two necklaces, the ones colored yellow (they also have diagonal line shading for those with black-and-white browsers). Note the zig-zag pattern that they follow, alternating between k-sets and (k+1)-sets. This is exactly a solution to the middle two levels problem.
It might be hoped that a general construction of symmetric Venn diagrams would give solutions to the middle two levels problem for n prime. However, a general construction of symmetric Venn diagrams seems very difficult, given that only one example is known for n=11, and none for any larger prime, so perhaps it's better to go the other way around. Maybe known solutions to the middle two levels problem for small values can give us insight into the construction of symmetric Venn diagrams!
Starting at the set {1}, and writing the bitstring representation of each subset we are lead to the table shown below (read down). Note that: (a) each of the 5 blocks is a right shift of the preceding block, (b) the columns are cyclicly equivalent (under a right shift of 6 bits), and (c) each block contains a representative of each non-trivial necklace of black and white beads. Such Gray codes are obviously balanced in the sense of Bhat and Savage [BS]; that is, each column has the same number of bit changes. It is easy to find symmetric Gray codes for n=7 using any of the Venn diagrams discussed earlier on this page. Gray codes with property (b) are said to be single-track. For more on single-track Gray codes see Hiltgen and Paterson, and Brandestini [HPB].
| 10000 | 01000 | 00100 | 00010 | 00001 |
| 10100 | 01010 | 00101 | 10010 | 01001 |
| 11100 | 01110 | 00111 | 10011 | 11001 |
| 11110 | 01111 | 10111 | 11011 | 11101 |
| 11010 | 01101 | 10110 | 01011 | 10101 |
| 11000 | 01100 | 00110 | 00011 | 10001 |
| Block 1 | Block 2 | Block 3 | Block 4 | Block 5 |
|---|
|
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. March 2001), DS #5. |
