

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. March 2001), DS #5. |
We follow Grünbaum [Gr75] in first defining a more general concept, an independent family. Let C = { C1, C2, ..., Cn } be a collection of simple closed curves drawn in the plane. The collection C is said to be an independent family if the intersection of X1, X2, ..., Xn is nonempty, where each Xi is either int(Ci ) (the interior of Ci ) or is ext(Ci ) (the exterior of Ci ).
If, in addition, each such intersection is connected and there are only finitely many intersections, then C is a Venn diagram, or an n-Venn diagram if we wish to emphasize the number of curves in the diagram. The condition that there are only a finite number of intersection points is usually assumed in the literature, but often not stated explicitly. It rules out segments of curves from intersecting.
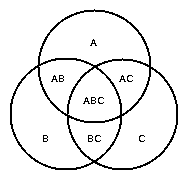
 On the left we show the most familiar of all Venn diagrams.
In this case n=3, the simple closed curves are all circles,
and in the leftmost diagram the 8 regions have been labelled with
the interiors that are included in each intersection.
The eighth region is the exterior region, corresponding to the empty set.
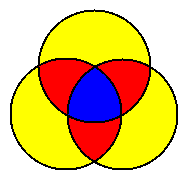
The colored diagram has all 1-sets colored yellow, all 2-sets red,
and the 3-set blue.
This diagram also occurs as a minimal projection of the
Borromean Rings.
On the left we show the most familiar of all Venn diagrams.
In this case n=3, the simple closed curves are all circles,
and in the leftmost diagram the 8 regions have been labelled with
the interiors that are included in each intersection.
The eighth region is the exterior region, corresponding to the empty set.
The colored diagram has all 1-sets colored yellow, all 2-sets red,
and the 3-set blue.
This diagram also occurs as a minimal projection of the
Borromean Rings.
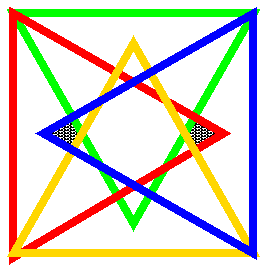 On the left we show an example, for n=4,
of an independent family that is not
a Venn diagram.
Here the simple closed curves are each congruent triangles, which
are colored red, blue, green, and gold.
Note that the intersection of the interiors of the red and
blue triangles with the exteriors of the green and gold
triangles gives a disconnected region, the shaded region(s)
in the figure.
On the left we show an example, for n=4,
of an independent family that is not
a Venn diagram.
Here the simple closed curves are each congruent triangles, which
are colored red, blue, green, and gold.
Note that the intersection of the interiors of the red and
blue triangles with the exteriors of the green and gold
triangles gives a disconnected region, the shaded region(s)
in the figure.
A simple Venn diagram is one in which no three (or more) curves intersect at a common point. Unless stated otherwise, we assume simple Venn diagams.
 Venn's construction, outlined in his original paper
[Ve80], is best
explained by considering the figure to the right.
Start with the 3 circle diagram.
Curves are successively added, with the new curve tracing the
one last added and dividing each existing region in two.
In the figure they are added in the order blue (4), red (5),
and green (6).
It should be clear where the seventh curve would be drawn.
Venn's construction, outlined in his original paper
[Ve80], is best
explained by considering the figure to the right.
Start with the 3 circle diagram.
Curves are successively added, with the new curve tracing the
one last added and dividing each existing region in two.
In the figure they are added in the order blue (4), red (5),
and green (6).
It should be clear where the seventh curve would be drawn.
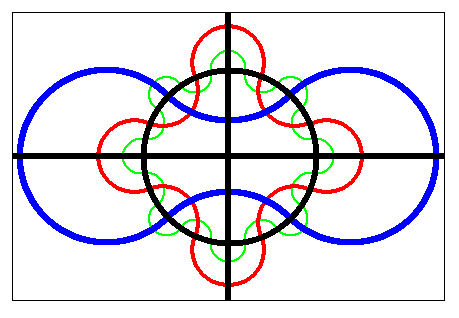
Anthony Edwards [Ed89a],
[Ed89b] developed another general
inductive construction that has several nice properties,
including some symmetry.
It is also best explained by means of an example; refer to
the diagram on the left.
For n=2 the diagram consists of two perpendicular lines.
(Strictly speaking we have to join the endpoints of these lines to make
them into simple closed curves.)
For n=3 a circle is added.
Successive curves will all be added that follow this circle,
weaving back and forth along the circle, again dividing each
region in two.
For n=4,5,6 the blue, red, and green curves are added,
in that order.
These diagrams have very attractive bipartite colorings as can be
seen below.
The reason for calling these colorings "bipartite" is explained in the
next section, Graphs Associated with Venn
Diagrams.

|
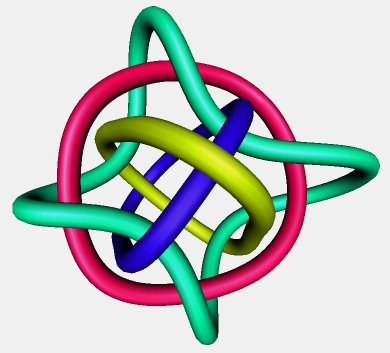
Every simple Venn diagram can be "woven" in to a link7; as one traverses any curve, the other curves alternately go over and under. The reader will find it an interesting exercise to prove that this is always possible for any collection of simple closed curves in the plane. For example, below we show the link that arises (after some smooth transformations in 3-space) from Venn's general construction for n = 4. This is clearly the same as the link that arises from Edward's general construction for n = 4, although the constructions give different links for n > 4.

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. March 2001), DS #5. |