
| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |
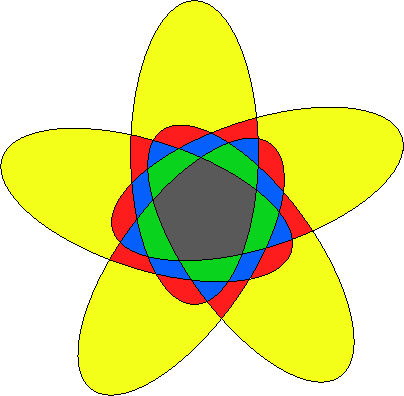 Here we (re-)show a Venn diagram made from 5
congruent ellipses.
The regions are colored according to the number
of ellipses in which they are contained: white (the external region) = 0, yellow = 1,
red = 2, blue = 3, green = 4, and black = 5.
Note that the number of regions colored with a given color corresponds to
the appropriate binomial coefficient: #(white) = #(black) = 1,
#(yellow) = #(green) = 5, and #(red) = #(blue) = 10.
Here we (re-)show a Venn diagram made from 5
congruent ellipses.
The regions are colored according to the number
of ellipses in which they are contained: white (the external region) = 0, yellow = 1,
red = 2, blue = 3, green = 4, and black = 5.
Note that the number of regions colored with a given color corresponds to
the appropriate binomial coefficient: #(white) = #(black) = 1,
#(yellow) = #(green) = 5, and #(red) = #(blue) = 10.
This diagram has a very a pleasing symmetry, namely an n-fold rotational symmetry. Such diagrams are said to be symmetric. This simply means that there is a point x about which the diagrams may be rotated by 2 π i / n and remain invariant, for i=0,1,...,n-1. Any symmetric Venn diagram must be made from congruent curves.
The purpose of this section is to survey what is known about symmetric diagrams.
Henderson first discussed the topic in his early paper [He], and he proved a simple necessary condition for the existence of symmetric Venn diagrams of n curves.
Theorem. A necessary condition for the existence of a symmetric n-Venn diagram is that n be a prime number.
To understand why the theorem is true, imagine the diagram to be split evenly into n sectors (pieces of pie). The C(n,k) 1 different regions representing the k-subsets must be evenly distributed in each of the n sectors. It thus follows that n divides C(n,k) for each k = 1,2,...,n-1. This divisibility restriction implies that n must be prime, via a theorem of Leibnitz [He, see also Ed96].
There is one other symmetry that we will consider for diagrams drawn in the plane. A symmetric Venn diagram has polar symmetry if it is invariant under "polar flips". Think of the diagram as being projected stereographically onto a sphere with the axis orthogonal to the plane running through the point of symmetry, and then project the diagram back onto the plane from the antipodal point on the axis. If the corresponding Venn dual graphs are isomorphic as plane graphs, then the diagram has polar symmetry. The symmetric Venn diagram shown above has polar symmetry, although it is perhaps not readily apparent.
Many symmetric diagrams are known for n = 2,3,5,7, and a few beautifully complex examples for n=11 (the large figure that appears twice in the title section of these pages, Victoria, is a simple polar symmetric 7-Venn diagram). These diagrams, along with counting results establishing the number of symmetric diagrams with different properties, can all be seen on this page:
| Examples of Symmetric Venn Diagrams for small n |
There are many extensions on the idea of symmetry in Venn diagrams and connected topics; a few are highlighted on the following page:
| Variants on Symmetry |
Extending symmetry to non-Venn diagrams is discussed on the section on symmetry on the page Generalizations and Extensions.
Recently, Jerrold Griggs, Chip Killian, and Carla Savage [GKS] made a major breakthrough by finding a construction for a symmetric Venn diagram for any prime n. The following page illustrates in detail the ideas used for the general construction:
| Symmetric Diagrams, Necklaces, and Chains |
Briefly, the idea is to create the dual graph of one sector of the diagram by building a series of chains that span a set of strings from the Boolean lattice, with the property that when this dual graph is rotated, the dual of the entire Venn diagram is created. The difficult part is specifying which strings to choose to form the appropriate subset (making up 1/nth of the Boolean lattice), using a known rule to build chains out of these strings, and then attaching them together and embedding them to form a planar dual of a sector of the diagram.
The diagrams produced by their construction are monotone and highly non-simple and have the property that there are n vertices through which all n curves pass. Their diagram for n=11 is shown on the page with examples of symmetric diagrams. The diagrams have exactly C(n, floor[ n/2 ] ) vertices, which is minimum for monotone Venn diagrams. In several ways their paper is the culmination of the last decade of research by several authors highlighted in these pages on generating symmetric Venn diagrams. The result has been widely publicised in the scientific press (see, for example, the articles [Ci03] and [Ci04]), and Donald Knuth presented the result in his annual "Christmas Tree" lecture in 2002 [KM].
In further work, Killian, Ruskey, Savage, and Weston [KRSW] showed that more vertices can be added to the construction by applying certain operations; see the bottom of the page on necklace diagrams for more details. The number of vertices can be increased to give asymptotically at least 2n-1 vertices; in practise the numbers are higher than 2n-1, at least for small n, but it appears to be difficult to prove a better bound.
The table below shows the highest known number of vertices in a symmetric diagram, for each n, versus the number of vertices in a simple diagram.
| n | vertices in simple symmetric diagram | best known | reference |
|---|---|---|---|
| 3 | 6 | 6 | 3-circle diagram |
| 5 | 30 | 30 | [Gr75] (the 5-ellipses diagram) |
| 7 | 126 | 126 | [Ed96], this survey |
| 11 | 2,046 | 1,837 | [HPS] (see this page) |
| 13 | 8,190 | 5,005 | [KRSW] |
| 17 | 131,070 | 81,787 | [KRSW] |
| 19 | 524,286 | 329,289 | [KRSW] |
Thus, the search for a simple symmetric Venn diagram of more than 7 curves continues.

| THE ELECTRONIC JOURNAL OF COMBINATORICS (ed. June 2005), DS #5. |