

| THE ELECTRONIC JOURNAL OF COMBINATORICS 4 (1997), DS #5. |
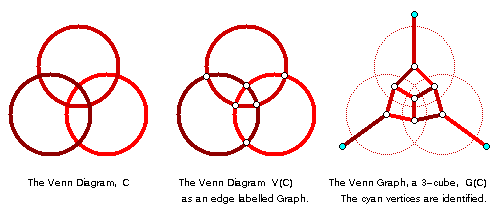
An n-Venn diagram C = {C1,...,Cn} may be regarded as a graph in two ways. The diagram itself can be thought of as an edge-colored plane5 graph V(C) whose vertices correspond to intersections of curves, and whose edges correspond to the segments of curves between intersections. Edges are colored according to the curve to which they belong. Following Chilakamarri, Hamburger, and Pippert [CHP], we overload the term and call this graph the Venn diagram. In an unlabelled Venn diagram we ignore the edge labels. As an example, the three circle Venn diagram has 6 vertices (corresponding to the 6 intersections) and 12 edges. Recall Euler's formula f = e - v + 2 relating the number of faces, edges, and vertices of a graph embedded in the plane. Assuming that no three curves intersect at a common point (i.e., a simple Venn diagram), we have e = 2v. By definition the number of faces is f = 2n. It thus follows that v = 2n - 2 and e = 2n+1 - 4 for simple Venn diagrams.
Two curves can meet at a point transversally or not, depending on whether the two curves cross. A moment's reflection will convince you that the curves in a simple Venn diagram must meet transversally. More generally, at any point of intersection in a Venn diagram, there must be at least two curves that meet transversally.
With each Venn diagram, C, we may associate another plane graph called the Venn graph, and denoted G(C), which is the planar dual of the Venn diagram. It's vertices are the connected open regions (faces) from the definition of Venn diagrams. Two vertices are connected by an edge if they share a common boundary. By default the edges are colored (by the color of the corresponding edge in the Venn diagram); if not, it is called an unlabelled Venn graph. For example, the unlabelled Venn graph of the three circle Venn diagram is an embedding of the 3-cube, Q3. Clearly, every n-Venn graph is a planar spanning subgraph of the n-cube, Qn. If C is a simple Venn diagram, then every face of G(C) is a quadrilateral, and thus is a maximal bipartite7 planar graph.
On the other hand, a Venn diagram may be embedded in the sphere via stereographic projection. In some sense it is more natural to look at Venn diagrams as being embedded on the sphere. Two Venn diagrams are in the same class if they can be projected to the same spherical Venn diagram.
The precise number of Venn diagrams and Venn classes has been determined by Chilakamarri, Hamburger and Pippert [CHP96b, HP96c, HP97a] for n = 1,2,3,4, and for simple diagrams and classes if n = 5. For n = 1,2 clearly there is only one diagram.
For n = 3 there are six distinct Venn classes and fourteen distinct Venn diagrams. Only one of the diagrams is simple (Class 6).
Note that classes 2 and 3 are equivalent but not isomorphic, as are diagrams #3.3 & #3.6 (and #3.4 & #3.5). It is interesting that diagrams #3.3 & #3.6 look identical with curves drawn in black and regions colored, even though the corresponding Venn diagrams are different. Diagram #3.3 appears also in [ES] (showing that it is a convex diagram). The diagrams in Class 2 have the property that each pair of curves at a point of intersection meet tranversally; the diagrams of Class 3 do not have this property.
For n = 4 there are two distinct simple Venn diagrams and one distinct Venn class (this was first observed by Grünbaum [Gr92a,p.8] and proven in [CHP96b]). Drawings of these two are shown in Figures 4 (a) and (b) in [Gr92a,p.7].
For n = 5, there are 11 distinct, reducible, simple Venn classes and 12 distinct, reducible, simple Venn diagrams. Drawings of these may be found in [HP96c]. There are 8 distinct simple, irreducible Venn classes ([CHP97a]). Five of them have one convex drawing in the plane. (Four of them were discovered by Grünbaum.) All five can be drawn with five congruent ellipses. Thus, in total, there are 19 simple Venn classes.
In proving these results several theorems of independent interest were proven:
Theorem H1. A simple Venn diagram for n > 2 is 3-connected.
A theorem of Whitney [Wh] states that a plane embedding of a 3-connected planar graph is unique, once the outer face has been identified. Thus, to determine whether two diagrams are in the same class, we need only try all possible embedings of one of them with each of its faces as the outer region and observe whether any of these embeddings is isomorphic to the other diagram.
Theorem H2. A simple Venn graph for n > 2 is 3-connected.
Theorem H3. No two curves of a Venn diagram belong to the same face.
A Venn diagram is reducible if the removal of one of its n curves results in a Venn diagram with n-1 curves. The two general constructions, by their nature, both yield reducible diagrams. A Venn diagram that is not reducible is irreducible. The ellipse diagram shown below is irreducible. For a long time it was not known whether a reducible Venn diagram whose curves are ellipses existed or not; such a diagram was recently discovered by Hamburger and Pippert [HP96a].
A n-Venn diagram C is extendible if there is a curve that can be added to it to make an (n+1)-Venn diagram, C'. Diagram C' is said to be an extension of C. Winkler [Wi] makes the following two observations:
Theorem W1. For n > 1, a simple n-Venn diagram C is extendible to a simple (n+1)-Venn diagram if and only if its Venn graph G(C) is Hamiltonian.
Theorem W2. If the n-Venn diagram C is an extension of an (n-1)-Venn diagram, then C is extendible to an (n+1)-Venn diagram.
To prove the later theorem, let B be the diagram whose extension is C. By Theorem W1, The curve H added to B to get C corresponds to a Hamiltonian cycle in G(B). In G(C), curve H becomes the prism4, P, of a cycle of length 2n. Since the prism of a cycle is Hamiltonian, C is extendible.
Edwards' general construction is a manifestation of this proof of Theorem W2, where the Hamilton cycle in P is the one that alternates back and forth between the two copies of the cycle, two vertices at a time from each cycle. Venn's general construction is related but different since it uses non-prism edges (example).
The proof of [CHP96] makes use of the radual graph, R(C) of the Venn diagram, which, for an arbitrary plane graph, is the union of the radial graph and the dual graph (see Ore [Or]). A simple example, using Venn diagram #3.4 is shown here. The strategy of their proof is first to show that R(C) is a simple triangulation and then invoke a theorem of Whitney [Wh] that any such graph is Hamiltonian. It is then easy to see that the Hamilton cycle in the radual graph can be used as the additional curve. This sufficient condition is also necessary as stated in this analogue of Theorem W1.
Theorem CHP1. For n > 1, a n-Venn diagram C is extendible to a (n+1)-Venn diagram if and only if its radual graph R(C) is Hamiltonian.
The first part of this section is more "geometric" than "graph theoretic". We introduce congruent Venn diagrams here because the examples are used to illustrate graph theoretic definitions.
 The general constructions of Venn and Edwards
outlined on the "What is a Venn Diagram" page
do not share a nice property of the first two
figures on the "What is a Venn Diagram" page
(made from circles and triangles),
namely, that they are constructed from
congruent2 curves.
In fact, Grünbaum
[Gr92b]
defines a Venn diagram to be nice
if it is made from congruent curves, but we'll prefer to
call them congruent Venn diagrams.
The general constructions of Venn and Edwards
outlined on the "What is a Venn Diagram" page
do not share a nice property of the first two
figures on the "What is a Venn Diagram" page
(made from circles and triangles),
namely, that they are constructed from
congruent2 curves.
In fact, Grünbaum
[Gr92b]
defines a Venn diagram to be nice
if it is made from congruent curves, but we'll prefer to
call them congruent Venn diagrams.
 On the right, we show a beautiful congruent Venn diagram made from 5
congruent ellipses.
The first such diagrams were constructed by
Grünbaum [Gr75].
The diagram above labels each region (except the very smallest,
where the labels wouldn't fit) with the labels of all ellipses
that contain the region.
In the second of the ellipse figures, the regions are colored
according to the number of ellipses in which they are
contained: grey = 0, yellow = 1,
red = 2, blue = 3, green = 4, and black = 5.
Note that the number of regions colored with a given color corresponds to
the appropriate binomial coefficient: #(grey) = #(black) = 1,
#(yellow) = #(green) = 5, and #(red) = #(blue) = 10.
On the right, we show a beautiful congruent Venn diagram made from 5
congruent ellipses.
The first such diagrams were constructed by
Grünbaum [Gr75].
The diagram above labels each region (except the very smallest,
where the labels wouldn't fit) with the labels of all ellipses
that contain the region.
In the second of the ellipse figures, the regions are colored
according to the number of ellipses in which they are
contained: grey = 0, yellow = 1,
red = 2, blue = 3, green = 4, and black = 5.
Note that the number of regions colored with a given color corresponds to
the appropriate binomial coefficient: #(grey) = #(black) = 1,
#(yellow) = #(green) = 5, and #(red) = #(blue) = 10.
| 1 | 2 | 3 | 4 | 5 |
| 12 | 13 | 15 | 25 | 45 | 14 | 34 | 35 | 23 | 24 |
| 123 | 135 | 125 | 245 | 145 | 134 | 345 | 235 | 234 | 124 |
| 1234 | 1235 | 1245 | 1345 | 2345 |
Because of the symmetry of the diagram, these circular listings have the property that they remain invariant when acted on by the cyclic permutation (1 2 3 4 5). Additonal examples of such revolving door lists may be constructed from the symmetric Venn diagrams on the next page.
A Venn diagram is monotone if, for 0 < k < n, every k-region is adjacent to both a (k-1)-region and a (k+1)-region. The general constructions of Venn and Edwards are monotone. Examples of non-monotone Venn diagrams may be found on the "Symmetric Venn Diagram" page. We know of no example of a simple monotone Venn diagram for which the k-regions, for some 0 < k < n, do not form a "cycle". Is there one?
We can view monotonicity in another way. The Venn graph, G(C), defined above, could also have been defined as a directed acyclic graph, with the direction indicating whether one vertex is a subset of another. Let's call this the directed Venn graph. The directed Venn graph is a spanning subgraph of the Hasse diagram (regarded as a directed graph) of the subset lattice. A Venn diagram is monotone if and only if the directed Venn graph has a unique maximum element (sink) and a unique minimum element (source).

| THE ELECTRONIC JOURNAL OF COMBINATORICS 4 (1997), DS #5. |