On the Codes Related to the Higman-Sims Graph
Abstract
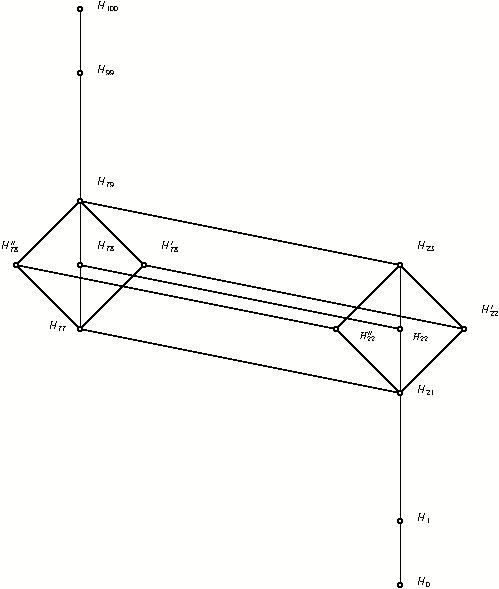
All linear codes of length $100$ over a field $F$ which admit the Higman-Sims simple group HS in its rank $3$ representation are determined. By group representation theory it is proved that they can all be understood as submodules of the permutation module $F\Omega$ where $\Omega$ denotes the vertex set of the Higman-Sims graph. This module is semisimple if $\mathrm{char} F\neq 2,5$ and absolutely indecomposable otherwise. Also if $\mathrm{char} F \in \{2, 5\}$ the submodule lattice is determined explicitly. The binary case $F = \mathbb{F}_2$ is studied in detail under coding theoretic aspects. The HS-orbits in the subcodes of dimension $\leq 23$ are computed explicitly and so also the weight enumerators are obtained. The weight enumerators of the dual codes are determined by MacWilliams transformation. Two fundamental methods are used: Let $v$ be the endomorphism determined by an adjacency matrix. Then in $H_{22} = \mathrm{Im} v $ the HS-orbits are determined as $v$-images of certain low weight vectors in $F\Omega$ which carry some special graph configurations. The second method consists in using the fact that $H_{23}/H_{21}$ is a Klein four group under addition, if $H_{23}$ denotes the code generated by $H_{22}$ and a "Higman vector" $x(m)$ of weight 50 associated to a heptad $m$ in the shortened Golay code $G_{22}$, and $H_{21}$ denotes the doubly even subcode of $H_{22}\leq H_{78} = {H_{22}}^\perp$. Using the mentioned observation about $H_{23}/H_{21}$ and the results on the HS-orbits in $H_{23}$ a model of G. Higman's geometry is constructed, which leads to a direct geometric proof that G. Higman's simple group is isomorphic to HS. Finally, it is shown that almost all maximal subgroups of the Higman-Sims group can be understood as stabilizers in HS of codewords in $H_{23}$.