Kauffman's Clock Lattice as a Graph of Perfect Matchings: a Formula for its Height

Abstract

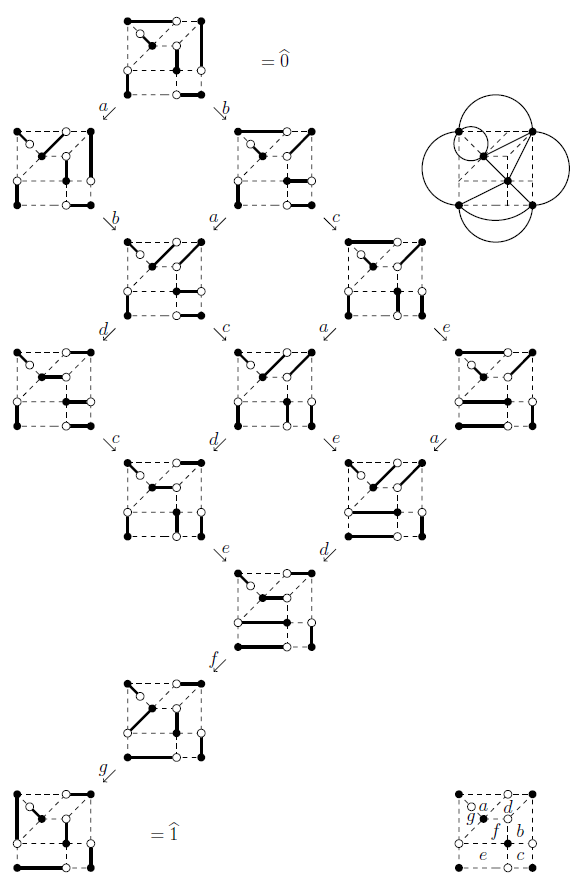
We give an algorithmic computation for the height of Kauffman's clock lattice obtained from a knot diagram with two adjacent regions starred and without crossing information specified. We show that this lattice is more familiarly the graph of perfect matchings of a bipartite graph obtained from the knot diagram by overlaying the two dual Tait graphs of the knot diagram. Furthermore we prove structural properties of the bipartite graph in general. This setting also makes evident applications to Chebyshev or harmonic knots, whose related bipartite graph is the popular grid graph, and to discrete Morse functions.